作者 Ivan Chien
始于 2022/01/12
分类：LeetCode
Tags: [ LeetCode ]

LeetCode 分类刷题 - 链表

按分类刷题，当前参考文章 https://labuladong.github.io/algo。

一些题目为二刷，以增强记忆、优化代码为主。

21. Merge Two Sorted Lists

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        // 要点 1
        ListNode* dummy = new ListNode(0);
        auto p = dummy;

        while (l1 != nullptr && l2 != nullptr) {
            if (l1->val < l2->val) {
                p->next = l1;
                l1 = l1->next;
            } else {
                p->next = l2;
                l2 = l2->next;
            }
            p = p->next;
        }

        // 要点 2
        p->next = l1 != nullptr ? l1 : l2;

        ListNode* ret = dummy->next;
        delete dummy;
        return ret;
    }
}

要点：

创建一个伪头结点，避免后面代码特别处理两个链表的头。C++ 注意要把动态分配的内存释放掉。
尾部一定为二选一，不解释。

23. Merge k Sorted Lists

struct Cmp {
    bool operator()(const ListNode* a, const ListNode* b) {
        return a->val > b->val;
    }
};
 
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode* dummy = new ListNode(-1);
        auto p = dummy;
				
      	// 要点
        priority_queue<ListNode*, vector<ListNode*>, Cmp> pq;
        for (auto l : lists) {
            if (l != nullptr)
                pq.push(l);
        }

        while (!pq.empty()) {
            auto front = pq.top();
            pq.pop();
            p->next = front;
            if (front->next)
                pq.push(front->next);
            p = p->next;
        }

        ListNode* ret = dummy->next;
        delete dummy;
        return ret;
    }
}

要点：

本题与 #21 唯一不同的地方在于需要使用优先队列。C++ 要构造一个存节点指针的优先队列比 Java 稍微麻烦一点，需要写一个 functor，上面的代码中为 Cmp。这个优先队列的顶，跟优先队列模板的 Compare 参数提供的 order 是相反的注意一下（我提供的是一个 greater 但是 top 返回给我的是小顶）。

141. Linked List Cycle

class Solution {
public:
    bool hasCycle(ListNode *head) {
        auto fast = head, slow = head;
				
      	// 要点 1
        while (fast != nullptr && slow != nullptr) {
            slow = slow->next;
          	// 要点 2
            if (fast->next == nullptr)
                return false;
            fast = fast->next->next;
          	// 要点 3
            if (fast == slow)
                return true;
        }

        return false;
    }
};

方法：

经典龟兔赛跑。

要点：

这题循环条件我看中文站官方题解好像可以用 slow != fast ，这样的话循环外返回 true 应该是也可以。
C++ 不能像 Java 一样莽着 .next。因为要访问 next 的 next 所以理所应当需要加一个判断。
本来我考虑了快慢指针撞结尾 null 的情况，但想了一下快指针永远在慢指针前面，所以撞是不可能撞的。

142. Linked List Cycle II

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        auto fast = head, slow = head;

        while (slow != nullptr && fast != nullptr) {
            slow = slow->next;
            if (fast->next == nullptr) return nullptr;
            fast = fast->next->next;
            if (slow == fast) break;
        }

				// 要点 1
        if (fast == nullptr) return nullptr;
				
      	// 要点 2
        slow = head;
        while (slow != fast) {
            slow = slow->next;
            fast = fast->next;
        }

        return slow;
    }
};

要点：

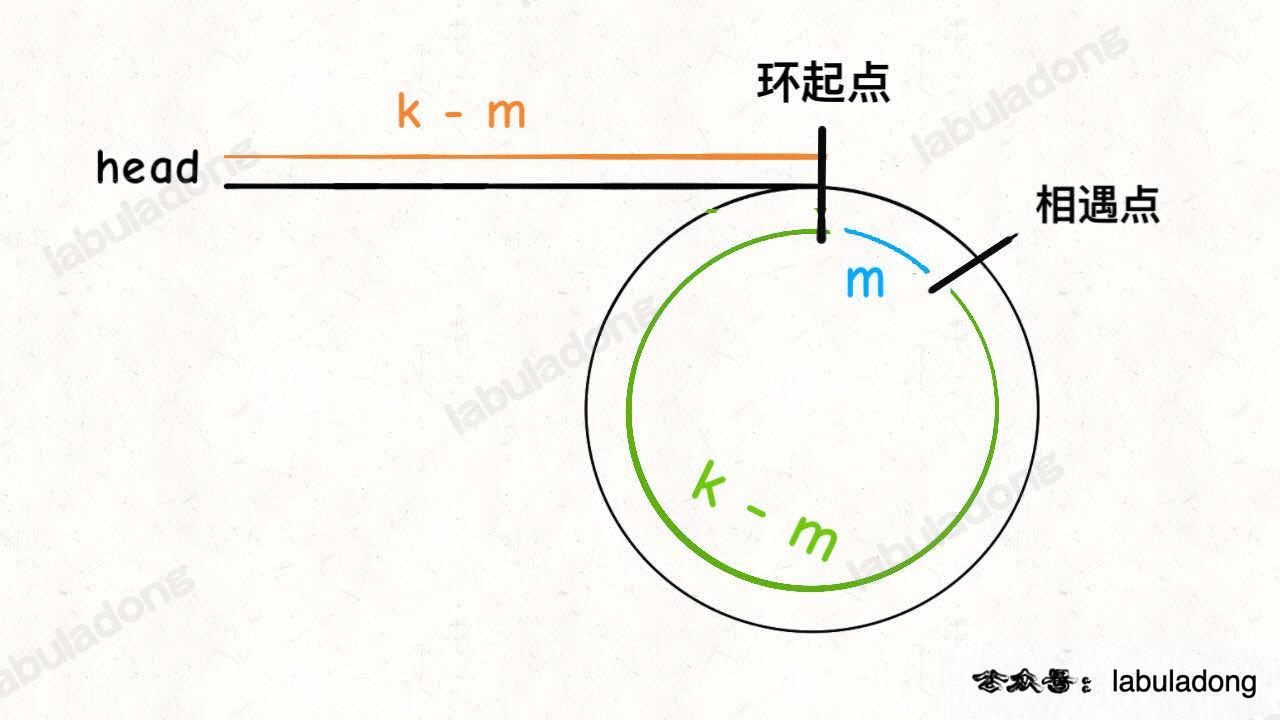
和 #141 不同的地方在于这里需要判断一下 fast 是否撞尾部了。不可能是 fast 的 next 撞，因为这样在第一个循环内已经 return 了。
这里用到的技巧是：

876. Middle of the Linked List

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        auto slow = head, fast = head;

        while (fast) {
          	// 要点
            if (!fast->next) break;
            slow = slow->next;
            fast = fast->next->next;
        }

        return slow;
    }
};

要点：

同样是快慢指针，不同于上面那个代码，最后的结果依赖于 slow 的值，所以这里 if-break 的位置需要考究，这里必须在 slow 更新前 break，才能保证在奇数个节点时 slow 的位置正确。

19. Remove Nth Node From End of List

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
      	// 要点 1
        auto front = head, back = head;
        while (n--) back = back->next;
      	// 要点 3
        if (!back) {
            auto next = head->next;
            delete head;
            return next;
        }
				
      	// 要点 2
        while (back->next) {
            front = front->next;
            back = back->next;
        }

        auto next = front->next;
        front->next = next->next;
        delete next;
        return head;
    }
}

要点：

前后指针。
确定我们要删除的不是 front->next 而不是 front。因为想删除 front 是不可能的。所以我这里选择判断 back 的下一项是否为 null，同理的方法还可以让 n 提前 -1 ，对应的代码修改逻辑也可。
为了保证要点 2 能够实现，要点 3 这里要特判 n 等于链表长度的情况。

160. Intersection of Two Linked Lists

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        auto a = headA, b = headB;
        
      	// 要点
        while (a != b) {
            if (a) a = a->next;
            else   a = headB;
            if (b) b = b->next;
            else   b = headA;
        }

        return a;
    }
}

方法：

本题的方法就是把两个链表拼在一起，一前一后两种拼法分别遍历。

要点：

a 等于 b 其实包含两种情况，也就是结果的两种情况：其一是到达相交点时，其二是都为 null 时。

206. Reverse Linked List

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr)
            return head;

        auto last = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return last;
    }
}

方法：

last 里面存放的是原链表尾，也就是结果的链表头。这个代码比较神奇的地方就在于它一直在更新的是 head->next->next，这句话的意思就是把 head 的 next 的 next 更新为自己，也就是将自己与后一个节点的位置调换，递归地从后往前进行。

这里有一个我以前写的版本，需要用到一个额外的局部变量来存储链表最后一个节点，因为我的 reverse 递归返回的不能是头结点而是尾节点。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr) return head;
        reverseListAux(head);
        return ret;
    }
    
    ListNode* reverseListAux(ListNode* head) {
        if (head->next == nullptr) return ret = head;
        auto rev = reverseListAux(head->next);
        head->next = nullptr;
        rev->next = head;
        return head;
    }

private:
    ListNode* ret;
};

92. Reverse Linked List II

class Solution {
public:
    ListNode* reverseN(ListNode* head, int n) {
        if (n == 1) {
            newHead = head->next;
            return head;
        }

        auto last = reverseN(head->next, n - 1);
        head->next->next = head;
        head->next = newHead;
        return last;
    }

    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if (left == 1) {
            return reverseN(head, right);
        }
        head->next = reverseBetween(head->next, left - 1, right - 1);
        return head;
    }

private:
    ListNode* newHead;
};

吐槽：

II 是 92 题，I 是 206 题，II 在 I 前面。

方法：

首先实现 reverseN。与完全 reverse 不同的地方在于，原首部需要指向的不再是 null 而是第 n + 1 个节点，所以存储第 n + 1 个节点到 newHead 变量里面。

再就是递归实现 reverseBetween。基础情况为 left == 1，也就是直接做 reverseN(head, right)。left 大于 1 的情况，通过递归将 head 后移，可以完成 [left, right] 区间的逆转，然后一路上把 next 接起来，顺路的 next 还是保持原来的值，位于 left 的 next 接到新的头上。

25. Reverse Nodes in k-Group

class Solution {
public:
  	// 要点 1
    ListNode* reverseRange(ListNode* head, ListNode* tail) {
        ListNode *pre, *cur, *nxt;
        pre = nullptr, cur = head;
        ListNode* oldHead = head;
        while (cur != tail) {
            nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        if (!head) return nullptr;
        auto p = head;
      	// 要点 2
        for (int i = 0; i < k; ++i) {
            if (!p) return head;
            p = p->next;
        }
      	// 要点 3
        auto newHead = reverseRange(head, p);
        head->next = reverseKGroup(p, k);
        return newHead;
    }
}

要点：

这里的函数 reverseRange，采用了迭代的方式对 [head, tail) 区间进行翻转，不接尾部，因为没用。
这个循环有两个作用，其一是判断剩余部分是否还有 k 个，另一是获得 reverseRange 的参数 tail 的值。
递归衔尾。

注意一下这个算法的时间复杂度仅为 $O(N)$，空间复杂度为 $O(1)$。

234. Palindrome Linked List

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        auto fast = head, slow = head;
        
        while (fast) {
            slow = slow->next;
            if (!fast->next) break;
            fast = fast->next->next;
        }
        
        auto left = head, right = reverse(slow);
        while (right) {
            if (left->val != right->val)
                return false;
            left = left->next, right = right->next;
        }
        return true;
    }

    ListNode* reverse(ListNode* head) {
        ListNode *pre, *cur, *nxt;
        pre = nullptr, cur = head;
        while (cur) {
            nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
}

虽然很简单，但是 Easy 就有点说不过去了吧 (— —

)。比较好的解法是将中点之后的部分翻转即可，找中点用龟兔。如果不能破坏原链表结构可以用递归回溯：

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        left = head;
        return backtrace(head);
    }

    bool backtrace(ListNode* right) {
        if (!right)
            return true;
        
        bool ret = backtrace(right->next);
        ret &= (left->val == right->val);
        left = left->next;
        return ret;
    }
    
private:
    ListNode* left;
};

递归回溯的方法虽然直观，但是效率不是特别高。

⇦ ⇨