作者 Ivan Chien
始于 
分类：PL
Tags: [ PL ]
程序语言理论和实现 Week 0 - 局部变量的语义与编译过程

Introduction to Language Design and Implementation - Part 2

Tiny Language 1

type rec expr =
    | Cst (int)
    | Add (expr, expr)
    | Mul (expr, expr)
    | Var (string)
    | Let (string, expr, expr)

type env= list<(string, int)>

let rec eval = (expr, env) => {
    switch expr {
    | Cst (i) => i
    | Add (a, b) => eval (a, env) + eval (b, env)
    | Mul (a, b) => eval (a, env) * eval (b, env)
    | Var(x) => assoc (x, env)
    | Let(x, e1, e2) => eval(e2, list{(x, eval(e1, env)), ...env})
    }
}

Formalization

terms: $e ::= \operatorname{Cst}(i) \mid \operatorname{Add}(e_1, e_2) \mid \operatorname{Mul}(e_1, e_2) \mid \operatorname{Var}(i) \mid \operatorname{Let}(x, e_1, e_2)$
envs: $\Gamma ::= \epsilon \mid (x, v) :: \Gamma$

Notations of the environment:

variable access: $\Gamma [x]$
variable update: $\Gamma [x := v]$

The evaluation rules:

\[\frac{}{\Gamma \vdash \operatorname{Cst}(i) \Downarrow i} \operatorname{E-const}\] \[\frac{\Gamma \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ \Gamma \vdash e_2 \Downarrow v_2}{\Gamma \vdash \operatorname{Add}(e_1, e_2) \Downarrow (v_1 + v_2)} \operatorname{E-add}\] \[\frac{\Gamma \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ \Gamma \vdash e_2 \Downarrow v_2}{\Gamma \vdash \operatorname{Mul}(e_1, e_2) \Downarrow (v_1 * v_2)} \operatorname{E-mul}\] \[\frac{\Gamma [x] = v}{\Gamma \vdash \operatorname{Var}(x) \Downarrow v} \operatorname{E-var}\] \[\frac{\Gamma \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ \Gamma [x := v_1]\vdash e_2 \Downarrow v_2}{\Gamma \vdash \operatorname{Let}(x, e_1, e_2) \Downarrow v_2} \operatorname{E-let}\]

$\vdash$ 叫 turnstile，$\LaTeX$ 记作 \vdash。

运行时靠变量名查环境表比较耗时，引入 partial evaluation，让编译器完成更多静态工作。

Tiny Language 2

module Nameless {
    type rec expr =
        | Cst (int)
        | Add (expr, expr)
        | Mul (expr, expr)
        | Var (int)
        | Let (expr, expr)
}

type env = list<int>

let rec eval = (expr : Nameless.expr, env) => {
    switch expr {
    | Cst (i) => i
    | Add (a, b) => eval (a, env) + eval (b, env)
    | Mul (a, b) => eval (a, env) * eval (b, env)
    | Var(n) => List.nth (env, n)
    | Let(e1, e2) => eval(e2, list{eval(e1, env)}, ...env)
    }
}

Semantics

envs: $s ::= \epsilon \mid v :: s$
\[\frac{}{s \vdash \operatorname{Cst}(i) \Downarrow i} \operatorname{E-const}\] \[\frac{s \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ s \vdash e_2 \Downarrow v_2}{s \vdash \operatorname{Add}(e_1, e_2) \Downarrow (v_1 + v_2)} \operatorname{E-add}\] \[\frac{s \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ s \vdash e_2 \Downarrow v_2}{s \vdash \operatorname{Mul}(e_1, e_2) \Downarrow (v_1 * v_2)} \operatorname{E-mul}\] \[\frac{s [i] = v}{s \vdash \operatorname{Var}(i) \Downarrow v} \operatorname{E-var}\] \[\frac{s \vdash e_1 \Downarrow v_1\ \ \ \ \ \ \ v_1 \cdot s\vdash e_2 \Downarrow v_2}{s \vdash \operatorname{Let}(e_1, e_2) \Downarrow v_2} \operatorname{E-let}\]

$s$ is a stack-like list, $v_1 \cdot s$ means stack push.

Explanation

原来的 $\Gamma$ 环境既包含「名字」又包含值，而「名字」实为静态的，在编译过程中即可处理掉。

接下来是将 expr 编译到 Nameless.expr：

Lowering expr to Nameless.expr

type cenv = list<int>

let rec comp = (expr: expr, cenv: cenv): Nameless.expr => {
    switch expr {
    | Cst (i) => i
    | Add (a, b) => Add(comp(a, cenv) + comp(b, cenv))
    | Mul (a, b) => Mul(comp(a, cenv), comp(b, cenv))
    | Var(x) => Var(index(cenv, x))
    | Let(x, e1, e2) => Let(comp(e1, cenv), comp(e2, list{x, ...cenv}))
    }
}

Similar to expr’s eval.

Compile Nameless.expr

为 stack machine 引入新的语义：

$(\operatorname{Var}(i); c, s) \rightarrow (c, s[i] :: s)$ (I-Var)
$(\operatorname{Pop}; c, n :: s)$ (I-Pop)
$(\operatorname{Swap}; c, n_2 :: n_1 :: s) \rightarrow (c, n_2 :: n_1 :: s)$ (I-Swap)

例子：

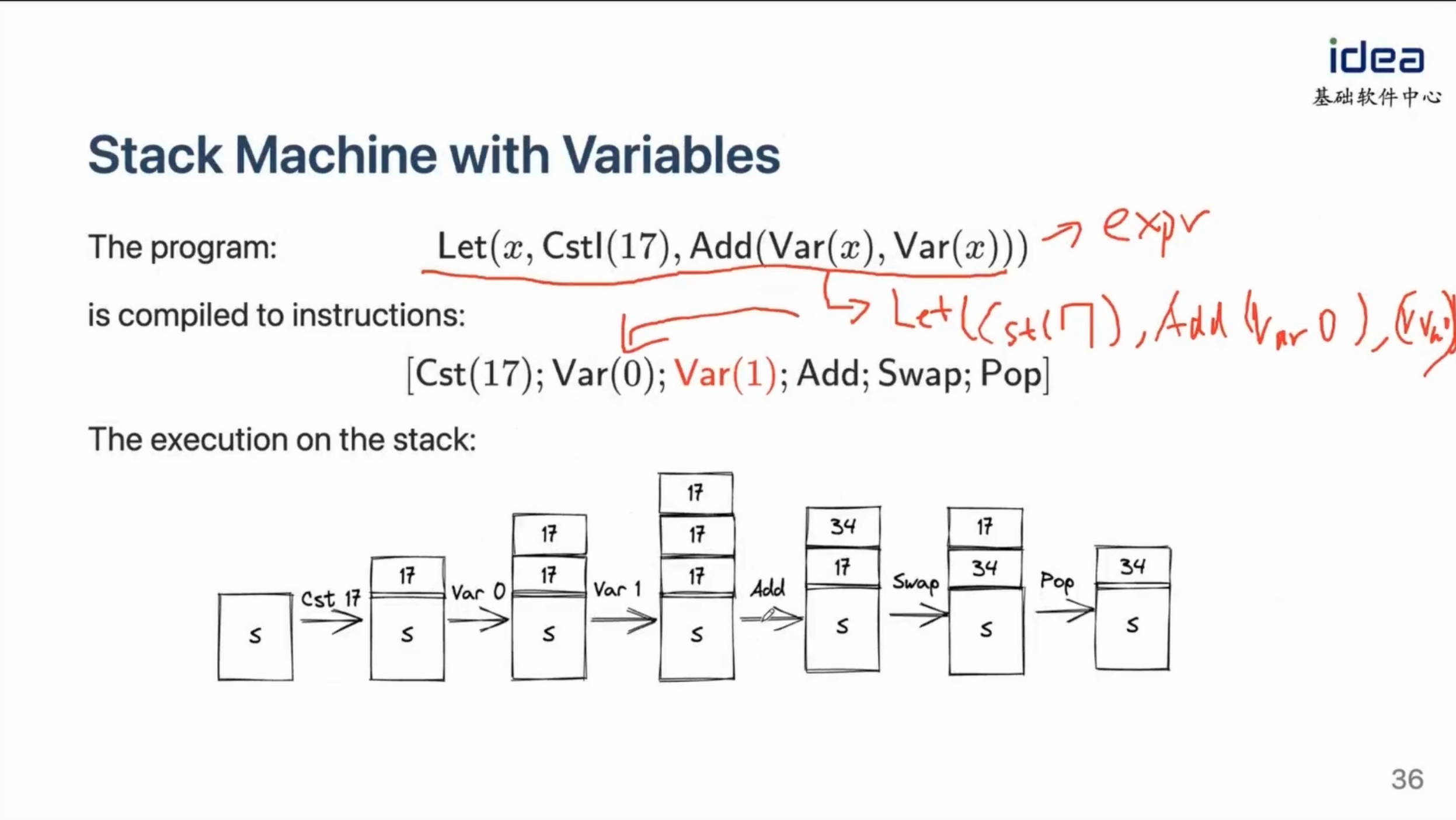
example1

Swap 和 Pop 的组合可以去除栈里留下的 $x$ 保留下 $v$。Swap 和 Pop 是为了保持栈平衡才引入的，因为 stack machine 的 eval 的最后结果一定会保证栈里的元素只有 1 个。所以需要 Swap & Pop 将「临时」存入栈的不需要的 local variable 的「值（value）」移除。

比如对应的上图中的 Cst(17) 临时入栈，是为了在后面的过程中，能把这个栈中的 17 当成「x」来使用。而后面的 Swap; Pop 针对的也就是这个 17。

关于红色的部分 Var(0) 为什么变成了 Var(1)，是因为 Var(0) 会伴随着 s[0] 入栈，但是这个下标就比较反传统的用线性表建栈的形式，因为传统我们用线性表作为栈的 push 是 s[len++] = x，栈底是不变的；而这里从头到尾都是 list {x, ...cenv}，栈顶永远是 0。类似 Lisp 的 (x . s)，然后取栈顶就是很简单的 (car s)。（所以说到底他用的就不是线性表而是单链表，用 C 写单链表做栈也得这样，主要的反直觉是在 C 的数组才用下标访问而不是链表）

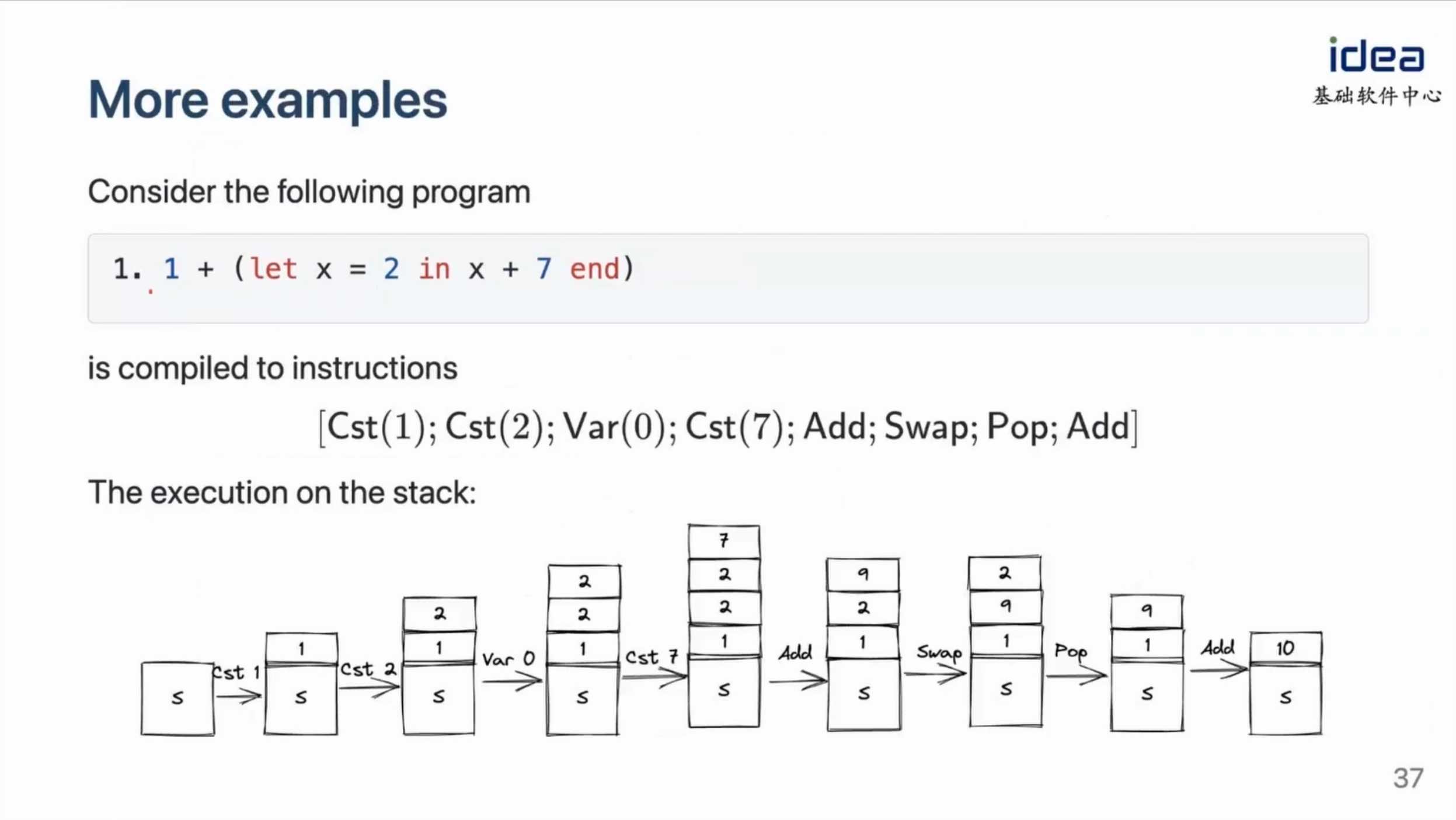
Another example:

example2

Summary

Q&A

先是问到类似 variable hiding 的代码是如何从 IR0 编译到 IR1 的。这里课里有说到，对于 Nameless.expr 名字变的不重要，两个 x 直接就是两独立的变量，如 $\Gamma$ 原本是 [(x, 2), (x, 1)]，到 $s$ 中就会被编译为 [2, 1]。

第二个问题没懂，问的是 IR0 -> IR1 的 comp 中怎么体现「静态」。我觉得可能想问的是编译程序是「动态」执行的，cenv 也在实时变化，那这个静态是体现在哪。

作业稍后。

Homework

let __nodebug = false

let separate = (info: string) => {
    Js.log("")
    Js.log(Js.String.repeat(2 + Js.String.length(info) + 2, "-"))
    Js.log("| " ++ info)
    Js.log(Js.String.repeat(2 + Js.String.length(info) + 2, "-"))
}

module Expr0 = {
    type rec expr =
        | Cst(int)
        | Add(expr, expr)
        | Mul(expr, expr)

    let rec eval = (expr: expr) => {
        switch expr {
        | Cst(i) => i
        | Add(a, b) => eval(a) + eval(b)
        | Mul(a, b) => eval(a) * eval(b)
        }
    }
}

separate("Expr0: (1 + 2) * 3 == 9")
let expr0: Expr0.expr = Mul(Add(Cst(1), Cst(2)), Cst(3))
Js.log(Expr0.eval(expr0))

module Instr0 = {
    type instr   = Cst(int) | Add | Mul
    type instrs  = list<instr>
    type operand = int
    type stack   = list<operand>

    let rec eval = (instrs: instrs, stack: stack) => {
        if !__nodebug {
            Js.log2("instrs:", instrs)
            Js.log2("stack:", stack)
            Js.log2("len of stack:", Belt.List.length(stack))
        }
        switch (instrs, stack) {
        | (list{Cst(i), ...rest}, s) =>
            eval(rest, list{i, ...s})
        | (list{Add, ...rest}, list{a, b, ...s}) =>
            eval(rest, list{a + b, ...s})
        | (list{Mul, ...rest}, list{a, b, ...s}) =>
            eval(rest, list{a * b, ...s})
        | (list{}, list{top, ...rest}) => {
            assert (0 == Belt.List.length(rest))
            top
        }
        | _ => assert false
        }
    }
}

separate("Instr0: (1 + 2) * 3 == 9")
// Notice: expr `a + b`, the `a` is pushed before `b`
let instr0: Instr0.instrs = list{Cst(1), Cst(2), Add, Cst(3), Mul}
Js.log(Instr0.eval(instr0, list{}));

module Expr0_Instr0 = {
    // hw2
    let rec compile = (expr: Expr0.expr): Instr0.instrs => {
        switch expr {
        | Cst(i) => list{ Cst(i) }
        | Add(a, b) => List.append(List.append(compile(a), compile(b)), list{ Add })
        | Mul(a, b) => List.append(List.append(compile(a), compile(b)), list{ Mul })
        }
    }
}

separate("Compile Expr0 -> Instr0: (1 + 2) * 3 == 9")
Js.log(Instr0.eval(Expr0_Instr0.compile(expr0), list{}))

module Expr1 = {
    type rec expr =
        | Cst(int)
        | Add(expr, expr)
        | Mul(expr, expr)
        | Var(string)
        | Let(string, expr, expr)

    type env = list<(string, int)>

    let rec eval = (expr: expr, env: env) => {
        switch expr {
        | Cst(x) => x
        | Add(a, b) => eval(a, env) + eval(b, env)
        | Mul(a, b) => eval(a, env) * eval(b, env)
        // List.assoc(x, env): get the corresponding value in env(which type is like [(key, value)]) where key is `name`
        | Var(name) => List.assoc(name, env)
        | Let(name, val, expr) => eval(expr, list{(name, eval(val, env)), ...env})
        }
    }
}

separate("Expr1: let x = 2 in x * (x + 3) == 10")
let expr1: Expr1.expr = Let("x", Cst(2), Mul(Var("x"), Add(Var("x"), Cst(2))))
Js.log(Expr1.eval(expr1, list{}))

module Nameless = {
    type rec expr =
        | Cst(int)
        | Add(expr, expr)
        | Mul(expr, expr)
        | Var(int)
        | Let(expr, expr)

    type env = list<int>
    let rec eval = (expr: expr, env: env) => {
        switch expr {
        | Cst(x) => x
        | Add(a, b) => eval(a, env) + eval(b, env)
        | Mul(a, b) => eval(a, env) * eval(b, env)
        | Var(i) => List.nth(env, i)
        | Let(val, expr) => eval(expr, list{eval(val, env), ...env})
        }
    }
}

separate("Nameless: let _0 = 2 in _0 * (_0 + 3) == 10")
let nameless: Nameless.expr = Let(Cst(2), Mul(Var(0), Add(Var(0), Cst(2))))
Js.log(Nameless.eval(nameless, list{}))

module Expr1_Nameless = {
    type nameList = list<string>

    let getIndexOfNameInList = (list: nameList, name: string) => {
        let rec aux = (list: nameList, idx: int) => {
            switch list {
            | list{x, ...rest} => {
                if x == name {
                    idx
                } else {
                    aux(rest, idx + 1)
                }
            }
            | list{} => assert false
            }
        }
        aux(list, 0)
    }

    // This is a trick which I used usually when I was implementing my version of C++ STL,
    // and the function named `aux` in `getIndexOfNameInList` above is also this trick called auxiliary functions
    let compile = (expr: Expr1.expr): Nameless.expr => {
        let rec compile = (expr: Expr1.expr, nameList: nameList): Nameless.expr => {
            switch expr {
            | Cst(x) => Cst(x)
            | Add(a, b) => Add(compile(a, nameList), compile(b, nameList))
            | Mul(a, b) => Mul(compile(a, nameList), compile(b, nameList))
            | Var(name) => Var(getIndexOfNameInList(nameList, name))
            | Let(name, val, expr) => Let(compile(val, nameList), compile(expr, list{name, ...nameList}))
            }
        }
        compile(expr, list{})
    }
}

separate("Compile Expr1 to Nameless: let x = 2 in x * (x + 3) == 10")
Js.log(Nameless.eval(Expr1_Nameless.compile(expr1), list{}))

// hw3-1
module Instr1 = {
    type instr   = Cst(int) | Add | Mul | Var(int) | Swap | Pop
    type instrs  = list<instr>
    type operand = int
    type stack   = list<operand>

    let rec eval = (instrs: instrs, stack: stack) => {
        if !__nodebug {
            Js.log2("instrs:", instrs)
            Js.log2("stack:", stack)
            Js.log2("len of stack:", Belt.List.length(stack))
        }
        switch (instrs, stack) {
        | (list{Cst(i), ...rest}, s) =>
            eval(rest, list{i, ...s})
        | (list{Add, ...rest}, list{a, b, ...s}) =>
            eval(rest, list{a + b, ...s})
        | (list{Mul, ...rest}, list{a, b, ...s}) =>
            eval(rest, list{a * b, ...s})
        | (list{Var(i), ...rest}, s) =>
            eval(rest, list{List.nth(s, i), ...s})
        | (list{Swap, ...rest}, list{a, b, ...s}) =>
            eval(rest, list{b, a, ...s})
        | (list{Pop, ...rest}, list{_, ...s}) =>
            eval(rest, s)
        | (list{}, list{top, ...rest}) => {
            // assert (0 == Belt.List.length(rest))
            Js.log("exec here")
            top
        }
        | _ => assert false
        }
    }
}

separate("Instr1: let x = 2 in x + x == 4")
let instr1: Instr1.instrs = list{Cst(2), Var(0), Var(1), Add, Swap, Pop}
Js.log(Instr1.eval(instr1, list{}))

// hw3-2
module Nameless_Instr1 = {
    type varType = VTemp | VLocal

    let findIndexInCombinedStack = (stack: list<varType>, i: int) => {
        let rec aux = (stack: list<varType>, ri: int, ii: int) => {
            switch stack {
            | list{VTemp, ...rest} => aux(rest, ri + 1, ii)
            | list{VLocal, ...rest} => {
                if ii == i {
                    ri
                } else {
                    aux(rest, ri + 1, ii + 1)
                }
            }
            | list{} => assert false
            }
        }
        aux(stack, 0, 0)
    }

    let compile = (expr: Nameless.expr): Instr1.instrs => {
        let rec compile = (expr: Nameless.expr, varTypes: list<varType>): list<Instr1.instr> => {
            if !__nodebug {
                Js.log2("expr:", expr)
                Js.log2("varTypes:", varTypes)
            }
            let ret: Instr1.instrs = switch expr {
            | Cst(x) => list{Cst(x)}
            | Add(a, b) => List.append(List.append(compile(a, varTypes), compile(b, list{VTemp, ...varTypes})), list{Add})
            | Mul(a, b) => List.append(List.append(compile(a, varTypes), compile(b, list{VTemp, ...varTypes})), list{Mul})
            | Var(i) => list{Var(findIndexInCombinedStack(varTypes, i))}
            | Let(val, expr) => List.append(List.append(compile(val, varTypes), compile(expr, list{VLocal, ...varTypes})), list{Swap, Pop})
            }
            if !__nodebug {
                Js.log2("ret:", ret)
            }
            ret
        }
        compile(expr, list{})
    }
}

// let nameless: Nameless.expr = Let(Cst(2), Mul(Var(0), Add(Var(0), Cst(2))))
separate("Compile Nameless -> Instr1: let _0 = 2 in _0 * (_0 + 3) == 10")
Js.log(Nameless_Instr1.compile(nameless))  // problem here

弄了好长时间，调不好。考研结束前我要是再弄这个我就是 **。