Names, Binders, De Bruijn Index

Church Numerals and Peano Numerals

let church_to_peano = (n) => n(x => S(x), Z)

let rec peano_to_church = (n) => {
    switch n {
    | Z => church_zero
    | S(n) => church_succ(peano_to_church(n))
    }
}

Church numerals 本质上是证明了 lambda calculus 的表达力，在实际中的用途可能不大。

Substitution with Non-closed Terms

这里可以参考一下我 TAPL 的笔记：

项的定义：设 $\mathcal{V}$ 是一个变量名的可数集合。项的集合是最小的集合 $\mathcal{T}$，若满足：

1. 对每个 $x \in \mathcal{V}$ ，$x \in \mathcal{T}$
2. 如果 $t_1 \in \mathcal{T}$ 并且 $x \in \mathcal{V}$，则 $\lambda x. t_1 \in \mathcal{T}$
3. 如果 $t_1 \in \mathcal{T}$ 并且 $t_2 \in \mathcal{T}$，则 $t_1\ t_2 \in \mathcal{T}$

定义：一个项 $t$ 的自由变量集合，记为 $FV(t)$，定义为：

• $FV(x) = {x}$
• $FV(\lambda x. t_1) = FV(t_1) \backslash {x}$
• $FV(t_1\ t_2) = FV(t_1) \cup FV(t_2)$

代换的定义：

• $[x \mapsto s] x = s$
• $[x \mapsto s] y = y\ \ (if\ y \neq x)$
• $[x \mapsto s] (\lambda y. t_1) = \lambda y. [x \mapsto s] t_1\ \ (if\ y \neq x\ \wedge\ y \notin FV(s))$
• $[x \mapsto s] (t_1\ t_2) = ([x \mapsto s]t_1)\ ([x \mapsto s]t_2)$

$\alpha$-conversion

简单说就是将 binders 改名。

let rename = (t, old, new) => {
    let rec go = (t) => {
        switch t {
        | Var(x) => if x == old { Var(new) } else { t }
        | Fn(x, a) => if x == old { Fn(new, go(a)) } else { Fn(x, go(a)) }
        | App(a, b) => App(go(a), go(b))
        }
    }
    go(t)
}

$\alpha$-equivalence

$\lambda x. M =_{\alpha} \lambda y. (M {y/x})$

其中 $M{y/x}$ 就是将 $M$ 中的 $x$ 都换成 $y$ 的 $\alpha$ 变换。

然后代换就可以表示为：

• $x{y/x} = y$
• $z{y/x} = z$
• $(MN){y/x} = (M{y/x})(N{y/x})$
• $(\lambda x. M){y/x} = \lambda y. (M{y/x})$
• $(\lambda z. M){y/x} = \lambda z. (M{y/x})$

这里只需要保证 y 这个符号在 M 中不存在或者直接生成一个独一无二的符号即可（如 Lisp 的 gensym、JavaScript 的 Symbol.new）。

// t[u/x] where u might have free variables
let rec subst = (t, x, u) => {
    switch t {
    | Var(y) => if x == y { u } else { t }
    | Fn(y, b) => if x == y { t } else {   // alpha conversion
        let y' = fresh_name()
        let b' = rename(b, y, y')
        Fn(y', subst(b', x, u))
    }
    | App(a, b) => App(subst(a, x, u), subst(b, x, u))
    }
}

注意到这里的：

    | App(a, b) => App(subst(a, x, u), subst(b, x, u))

App 中的 a 和 b 会做一个递归的相同的操作，这样的操作是 trivial 的（我不知道什么样的具体才叫 trivial），这里可以使用 visitor pattern 去简化重复的操作。

De Bruijn Index

德布朗指数就是静态距离，或者是指当前位置到对应 binder 的相对距离。比如 $\lambda x. \lambda y. x \ (y\ x)$ 可以表示为 $\lambda . \lambda . 1\ (0\ 1)$。

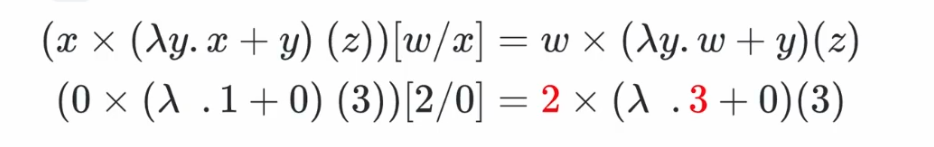
比如这里的 $w$ 使用 de Bruijn Index 2 替换 $x$ 对应的 0，但是因为进入括号后又会遇到一个新的 binder（是由 $\lambda$ 给出的），所以相对距离（或者说深度）也要相对地加 1 变成 3。

// t[u/i]: use u to replace Var(i) in term t
let rec subst = (t, i, u) => {
    switch t {
    | Var(j) => if j == i { u } else { t }  // 这里好像错了，应该是 t - 1，在 HW 里有
    | Fn(b) => Fn(subst(b, i + 1, shift(1, u)))
    | App(a, b) => App(subst(a, i, u), subst(b, i, u))
    }
}

Shift

比如：

这个 shift 只作用于 unbound variables。比如：

为此引入一个 cutoff：

• $\uparrow^i_d(j) = j, j < d$
• $\uparrow^i_d(j) = i + j, j \geq d$
• $\uparrow^i_d(\lambda. t) = \lambda. \uparrow^i_{d+1}(t)$
• $\uparrow^i_d(t_1 t_2) = \uparrow^i_d(t_1) \uparrow^i_d(t_2)$

d 表示的是穿过 binder 的个数，如果这中间有一个变量 i 是小于 d 的，那肯定就代表这个 i 是自由变量。

代码表示为 shift_aux(i, d, t)，其中 d 表示 cutoff。shift(i, t) = shift_aux(i, 0, t)。

HW

-- Complete the de Bruijn index based interpreter in natural semantics
-- Apply the de Bruijn index for extended lambda calculus (+ Let)

data DeBruijn
    = Var Integer
    | Fun DeBruijn
    | App DeBruijn DeBruijn
    | Let DeBruijn DeBruijn
    deriving Show

shift :: Integer -> DeBruijn -> DeBruijn
shift i = shiftAux i 0
    where shiftAux :: Integer -> Integer -> DeBruijn -> DeBruijn
          shiftAux i d t@(Var j) = if j < d then Var j else Var $ i + d
          shiftAux i d t@(Fun body) = Fun $ shiftAux i (d + 1) body
          shiftAux i d t@(App a b) = App (shiftAux i d a) (shiftAux i d b)
          shiftAux i d t@(Let val body) = Let (shiftAux i d val) (shiftAux i (d + 1) body)

-- t[u/x]
subst :: DeBruijn -> Integer -> DeBruijn -> DeBruijn
subst t@(Var i) x u = if i == x then u else Var $ i - 1  -- 这里在想了想应该是 i - 1 才对吧
subst t@(Fun body) x u = Fun $ subst body (x + 1) $ shift 1 u
subst t@(App a b) x u = App (subst a x u) (subst a x u)
subst t@(Let val body) x u = Let (subst val x u) (subst body x u)

eval :: DeBruijn -> DeBruijn
eval v@(Var i) = v
eval f@(Fun body) = Fun $ eval body
eval a@(App f arg) = eval $ subst ef 0 earg
    where (Fun ef) = eval f
          earg = eval arg
eval l@(Let val body) = eval $ App (Fun body) val

churchTrue = Fun $ Fun $ Var 1
churchFalse = Fun $ Fun $ Var 0
ifThenElse = Fun $ Var 0

-- test = eval $ Let churchTrue $ Let churchFalse $ Var 1
test = eval $ Let churchFalse $ Let churchTrue $ App (App (App ifThenElse churchTrue) $ Var 1) $ Var 0

main :: IO ()
main = print test