Static Program Analysis - Data Flow Analysis - Foundations

https://cs.nju.edu.cn/tiantan/software-analysis/DFA-FD.pdf

Maths

Partial Order

We define poset as a pair $(P, \sqsubseteq)$ where $\sqsubseteq$ is a binary relation that defines a partial ordering over $P$, and $\sqsubseteq$ has the following properties:

1. Reflexivity. $\forall x \in P, x \sqsubseteq x$
2. Antisymmetry. $\forall x, y \in P, x \sqsubseteq y \wedge y \sqsubseteq x \Rightarrow x = y$
3. Transitivity. $\forall x, y, z \in P, x \sqsubseteq y \wedge y \sqsubseteq z \Rightarrow x \sqsubseteq z$

partial means for a pair of set elements in P, they could be incomparable.

Upper and Lower Bounds

Given a poset $(P, \sqsubseteq)$ and its subset $S$ that $S \sqsubseteq P$, we say that:

• $u \in P$ is an upper bound of $S$, if $\forall x \in S, x \sqsubseteq u$
• $l \in P$ is an lower bound of $S$, if $\forall x \in S, l \sqsubseteq x$

Define the least upper bound (lub or join) of $S$, written $\sqcup S$, if for every upper bound of $S$, say $u$, $\sqcup S \sqsubseteq u$. The greater lower bound (glb or meet) of $S$, written $\sqcap S$, if for every lower bound of $S$, say $l$, $l \sqsubseteq \sqcap S$.

If $S$ contains only two elements a and b ($S = {a , b}$), then:

• $\sqcup S$ can be written $a \sqcup b$ (the join of $a$ and $b$)
• $\sqcap S$ can be written $a \sqcap b$ (the meet of $a$ and $b$)

Properties:

1. Not every poset has lub or glb
2. But if a poset has lub or glb, it will be unique

Lattice

Given a poset $(P, \sqsubseteq)$, $\forall a, b \in P$, if $a \sqcup b$ and $a \sqcap b$ exist, then $(P, \sqsubseteq)$ is called a lattice.

Complete Lattice

Given a lattice $(P, \sqsubseteq)$, for arbitrary subset $S$ of $P$, if $\sqcup S$ and $\sqcap S$ exist, then $(P, \sqsubseteq)$ is called a complete lattice.

Every complete lattice $(P, \sqsubseteq)$ has a greatest element $\top = \sqcup P$ called top and a least element $\bot$ called bottom.

Product Lattice

• A product lattice is a lattice
• If a product lattice $L$ is a product of complete lattices, then $L$ is also complete

Data Flow Analysis Framework via Lattice

Monotonicity

A function $f: L \rightarrow L$ ($L$ is a lattice) is monotonic if $\forall x, y \in L$, $x \sqsubseteq y \Rightarrow f(x) \sqsubseteq f(y)$

Fixed-point Theorem

Relate Iterative Algorithm to Fixed-point Theorem

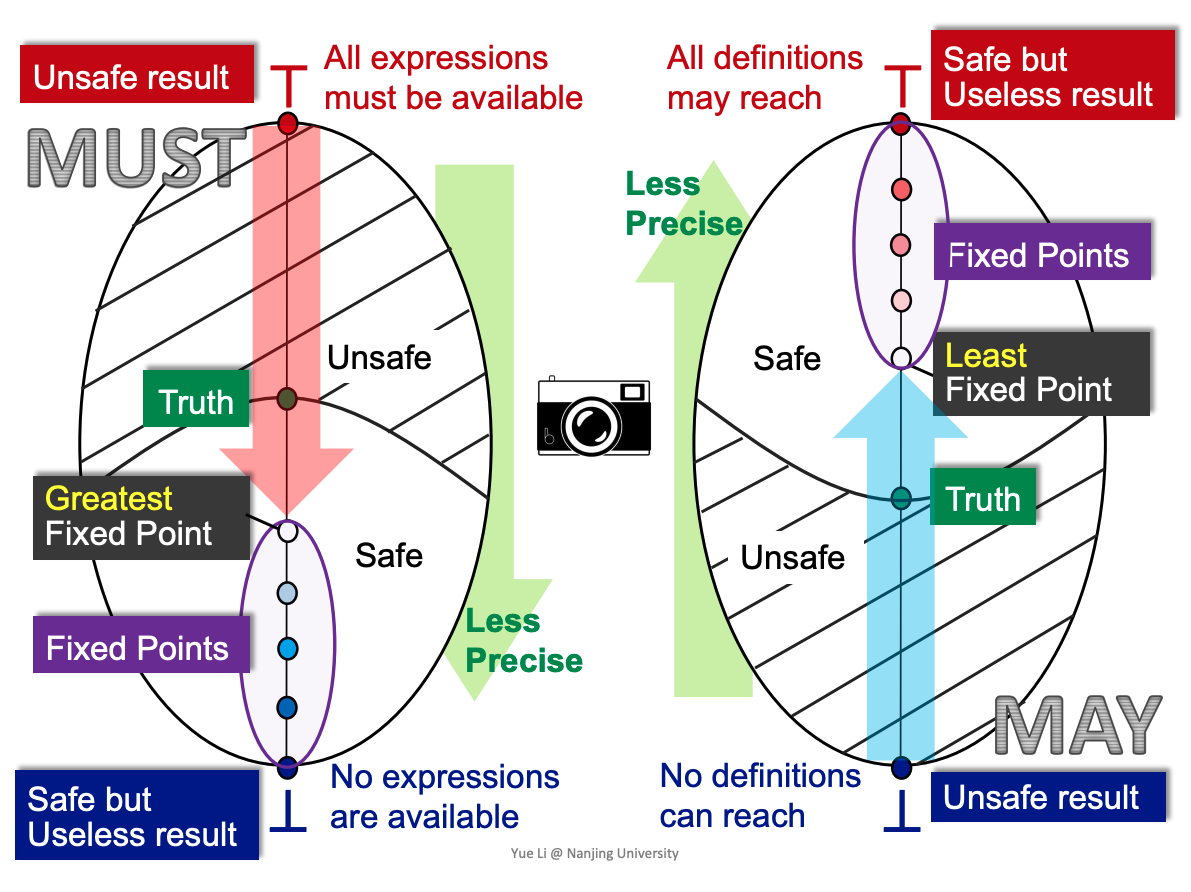
May and Must Analyses, a Lattice View

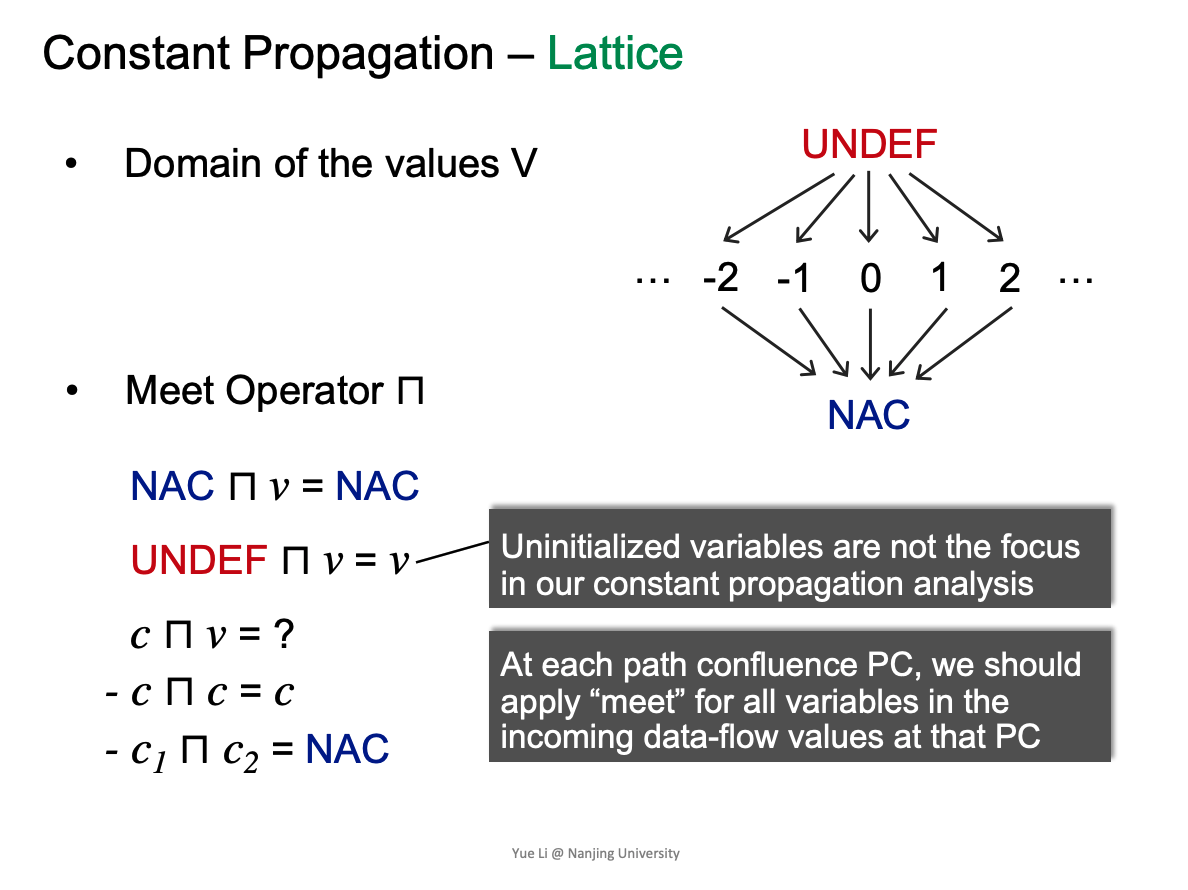
Constant Propagation

Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p.

Must analysis. Forwards.

Worklist Algorithm, an Optimization of Iterative Algorithm